Ci si domanderà cosa c’entra il QRP con il tessuto che ricopre il nostro corpo.
In effetti il riferimento è all’ effetto pelle (in inglese Skin Effect), cioè alla proprietà di un conduttore di confinare la corrente elettrica a frequenze elevate solamente in un sottilissimo strato appena sotto la superficie. L’argomento è molto ampio e complesso e qui rischiamo di essere troppo semplicisti. Cerchiamo comunque di avventuraci in questo terreno della fisica almeno in alcuni concetti principali, senza entrare in formule complesse.
Quando lavoriamo con corrente continua, e fino poco sopra le frequenze audio, siamo abituati a considerare che tanto maggiore è la sezione del nostro conduttore, tanto minore sarà la resistenza che questo offre al passaggio della corrente e quindi tanto minori saranno le perdite di energia per “effetto Joule” (in pratica, una parte della potenza applicata se ne va a riscaldare l’universo). In questo caso la corrente continua, o a bassa frequenza, scorre attraverso tutta la sezione del conduttore.
Se il conduttore è lungo “L” [m], ha sezione “S” [m2] ed è costituito da un materiale con resistività ρ [Ω m], allora la sua resistenza, che in c.c. è il rapporto fra tensione applicata e corrente che scorre, vale
R = V/I = ρ L / S
e l’unità di misura è l’ohm Ω. Quindi in C.C., a parità di ρ, la resistenza R è direttamente proporzionale alla lunghezza ed inversamente proporzionale alla sezione. Quando impieghiamo un conduttore per le realizzazioni in C.C. o frequenze audio, per ridurre la sua resistenza basta aumentarne la sezione.
La tabella riporta, come esempio, i valori (approssimati e in ordine crescente) di resistività in C.C. a 20°C per alcuni materiali (i valori sono in nano ohm-metro; fonte CRC Handbook of Chemistry and Physics):
| Materiale | Resistività ρ (Ωm x 10-9) @ 20°C |
| Argento | 16 |
| Rame | 17 |
| Oro puro | 24 |
| Alluminio | 28 |
| Ottone | 70 |
| Bronzo fosforoso | 78 |
| Ferro 98% | 100 |
| “Constantana” (60% rame; 40% nichel) | 490 |
| Nickel-cromo (80% nichel, 20% cromo) | 1000 |
Lavorando (grossomodo) da 1 MHz in su, dipendendo dalla misura del conduttore, a causa dell’Effetto Pelle tutta la corrente fluirà in uno strato sottilissimo appena sotto la superficie. Ad esempio, a 10 MHz, in un conduttore di rame la corrente a radio frequenza applicata scorre in uno strato profondo appena 2 centesimi di millimetro (0,02 mm). Questo strato in cui fluisce la radiofrequenza si dice “spessore della pelle”, traduzione dell’inglese “skin depth”, indicato con il simbolo δ.
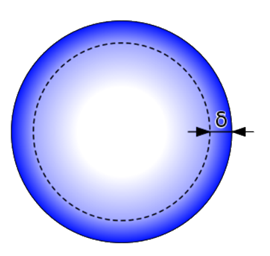
Alle frequenze di impiego radioamatoriale risulta che il valore di δ (“delta”) in funzione della frequenza f, della permeabilità µ (“mho”) e della resistività ρ “rho” , vale
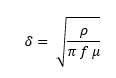
Da formule che non si presentano, risulta che per ogni multiplo di δ la densità di corrente a tale distanza dalla superficie vale circa 0,37 volte la densità di corrente che vi è nella superficie.
Lo spessore δ, a parità di parametri µ e ρ, varia con il reciproco della radice quadrata della frequenza, decrescendo velocemente all’aumentare di f (v. esempio in tabella per range 1 – 10 – 100 MHz)
| f [Hz] | δ [mm] |
| 1.000.000 | 0,07 |
| 10.000.000 | 0,02 |
| 100.000.000 | 0,01 |
Nelle nostre HF e VHF la radiofrequenza scorre grossomodo in uno strato spesso da 2 a 1 centesimi di millimetro.
È possibile calcolare, in via teorica, la resistenza in A.C. di un conduttore partendo dalla sua resistenza in D.C. e dalla conoscenza dello spessore δ. La resistenza effettiva dovuta a una corrente confinata vicino alla superficie di un grande conduttore (molto più spesso di δ) può essere determinata come se la corrente scorresse uniformemente attraverso uno strato di spessore δ in base alla resistività in C.C. del materiale. L’area della sezione trasversale effettiva è approssimativamente uguale a δ volte la circonferenza del conduttore. Quindi un lungo conduttore cilindrico come un filo, avente un diametro D molto grande rispetto a δ , ha una resistenza approssimativamente uguale a quella di un tubo cavo con spessore di parete δ che trasporta corrente continua. La resistenza AC di un filo di lunghezza l e resistività ρ è:
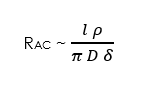
In campo radio-ingegneristico, e in particolare dal nostro punto di vista di radioamatori querreppisti, la conseguenza più importante è che il conduttore, ad esempio quello che utilizziamo per realizzare le antenne, presenta una resistenza maggiore alle alte frequenze che non alla corrente continua (che è quella che misuriamo con un semplice ohmmetro in CC). Il fenomeno dell’effetto pelle è la principale causa delle perdite di energia nelle linee di trasmissione, nelle antenne, nelle bobine.
A volte leggiamo indicazioni di impiegare filo con diametro ridotto per ridurre il peso o la dimensione della bobina negli accordatori, nelle trappole per antenne, del radiatore d’antenna. Dal punto di vista radio-tecnico-qrp non è un buon consiglio: i nostri già pochi watt verranno decurtati di una quota che se ne andrà in calore. Non sarà grande, ma pur sempre esiste.
Un po’ di teoria per chi vuole leggere.
A cosa è dovuto l’effetto pelle? Dobbiamo riprendere, per chi la aveva, qualche nozione di fisica.
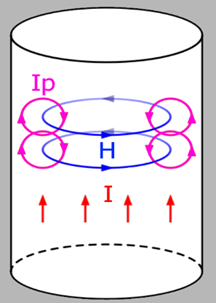
Con riferimento al disegno, una corrente I in un conduttore produce un campo magnetico H dentro e intorno al conduttore. Viceversa, un campo magnetico variabile induce nel conduttore una corrente variabile, alla stessa frequenza. Quando l’intensità della corrente I in un conduttore cambia (corrente alternata), cambia anche il campo magnetico. La variazione del campo magnetico a sua volta crea un campo elettrico che si oppone alla variazione dell’intensità della corrente I. Questo campo elettrico opposto è chiamato “forza controelettromotrice” (FCEM) che risulta essere più intensa al centro del conduttore. Si generano delle correnti parassite Ip che annullano parzialmente il flusso di corrente I al centro e lo rinforzano vicino alla pelle. In altre parole, gli elettroni conduttori vengono spinti a “viaggiare” sulla superficie del conduttore.
Qui mi fermo perché la cosa si fa pesantuccia, ma non posso non dire che quanto sopra descritto vale per un conduttore isolato. Nei conduttori intrecciati (il classico filo di rame per impianti elettrici che usiamo per le antenne filari) si aggiunge l’“effetto prossimità” fra i singoli trefoli che complica il discorso e fa sì che anziché il diametro sia più importante il perimetro del conduttore complessivo.
E non dimentichiamo poi che l’effetto pelle è la causa del disadattamento che si genera quando alimentiamo un’antenna bilanciata come il dipolo con un cavo sbilanciato come il cavo coassiale. Questo perché, dal punto di vista della radiofrequenza, il cavo coassiale presenta 3 percorsi per il segnale, con tutto quello che ne consegue: il centrale, la parte interna della calza e la parte esterna della calza.
Riferimenti:
- The ARRL Handbook for Radio Communications
- Transmission Lines and Networks, Walter C. Johnson, McGraw-Hill
- Wikipedia
73 de I3NJI Vitaliano